ECC, ECDSA 이해하기 (ft. 수학)

ECC, ECDSA 이해하기 (ft. 수학)

0. 목적

ECDSA 작동 방식, 알고리즘, 디지털 서명 확인 방법 및 그러한 서명을 위조하는 것이 불가능한 방법을 설명한다.

기본 내용

• ECDSA는 정수만 사용(실수는 사용하지 않는다)
• 일반적으로 ECDSA는 총 160bits를 사용(49자릿수)

1. 필요한 수학 개념

Modular

한 방향으로는 쉽지만 다른 방향으로는 어려운 일방향 함수를 고안하기 위해 탄생되었다.
시계 연산으로도 알려져있다.

$$x\ mod\ p$$
$$46\ mod\ 12 \equiv 10$$

Modular 합동

정수 $a, b$ 와 양의 정수 $m$에 대하여 $a-b$가 $m$으로 나누어 떨어진다면, $a$와 $b$ 는 모듈로 $m$ 합동(a is congruent to b modulo m)이다.

$$a\equiv b\ (mod\ m)$$

Modular 합동의 필요충분조건

$a\equiv b\ (mod\ m)$의 필요충분조건은, $a\ mod\ m = b\ mod\ m$이다.

정수 $a, b$가 모듈로 $m$ 합동이기 위한 필요충분조건은, $a = b+km$을 만족하는 $k$의 존재이다.
($a-b=km$이란 뜻이므로 합동의 정의와 같다)

Modular 사칙연산

$$\begin{matrix}
(a+b)\ mod\ m&=&((a\ mod\ m)+(b\ mod\ m))\ mod\ m\
(a-b)\ mod\ m&=&((a\ mod\ m)-(b\ mod\ m))\ mod\ m\
(a\times b)\ mod\ m&=&((a\ mod\ m)\times(b\ mod\ m))\ mod\ m\
(a\div b)\ mod\ m&=&((a\ mod\ m)\div(b\ mod\ m))\ mod\ m ????
\end{matrix}$$

사칙연산 중 나눗셈에 닫혀있다.
역원의 곱셈으로 변경하면 성립된다.

$$\begin{matrix}
(a\div b)\ mod\ m &=& (a\times b^{-1})\ mod\ m\
&=&((a\ mod\ m)\times(b^{-1}\ mod\ m))\ mod\ m
\end{matrix}$$

Modular 역원

$b^{-1}$은 모듈러 group 중에서 $b$와 곱하고 모듈러를 취했을 때 $1$이되는 값이다.

$$(b\times b^{-1})\ mod\ m \equiv 1$$

$m$과 서로소인 수($m$과 공통 소인수가 없는 수)만 모듈러 역원($mod\ m$)을 가진다.

모듈러 group에서 곱셈에 대한 역원을 구하는 방법은 여러가지가 있다.
가장 무식하게는 group 내 모든 원소($0$ ~ $m-1$)에 대해서 곱셈을 해본 후 모듈러를 취했을때 1이 나오는 값을 찾으면 된다.

하지만 수학적으로 더 빠르게 구할 수 있는 방법을 알아보자.

페르마의 소정리

정수 $a$를 선택해서 거듭제곱 $a^2, a^3, a^4 ... (mod\ p)$를 계산하면 어떤 규칙성이 있는가?

패턴을 찾으면, $a\equiv 0$이 아니면 $a^2\equiv 1\ (mod\ 3), a^4\equiv 1\ (mod\ 5), a^6\equiv 1\ (mod\ 7)$

소수 $p$와 서로소인 정수 $a$에 대해 다음과 같은 식이 존재한다.

$$a^{p-1}\equiv 1\quad (mod\ p) $$

$$a^p\equiv a\ mod\ p$$

식을 전개하면,

$$a^{p-1}=a\times a^{p-2}\equiv 1 \ (mod\ p)$$

$a의$ 역원을 한번에 구할 수 있다. ($a^{p-2}$)

단, $m$은 소수여야하고 $a$는 $m$과 서로소라는 가정이 충족되어야 한다.

다시 구하려던 식을 정리해보자.

$$\begin{matrix}
(a\div b)\ mod\ m &=& (a\times b^{-1})\ mod\ m\
&=&((a\ mod\ m)\times(b^{-1}\ mod\ m))\ mod\ m\
&=&((a\ mod\ m)\times(b^{m-2}\ mod\ m))\ mod\ m
\end{matrix}$$

소스코드

재귀

long long get_pow(long long a, long long b, long long mod){
    if(b==0) return 1;
    if(b&1) return a * get_pow(a*a%mod, (b-1)/2, mod) % mod;
    return get_pow(a*a%mod, b/2, mod) % mod;
}

long long mod_inverse(long long a, long long mod){
    long long b = mod-2;
    return get_pow(a,b,mod);
}

반복문

long long mod_inverse(long long a, long long mod){
    long long ret = 1;
    int b = mod-2;
    while(b!=0){
        if(b&1) ret = (ret*a)%mod;
        a = (a*a)%mod;
        b>>=1;
    }
    return ret;
}

확장 유클리드 알고리즘

페르마의 소정리는 $m$이 소수라는 제약조건이 있다.

확장 유클리드 호제법은 $m$이 소수가 아니어도 $a$와 $m$이 서로소라는 조건만 만족하면 곱셈에 대한 역원을 구할 수 있다.

확장 유클리드 알고리즘(Extended Euclidian Algorithm)은 유클리드 호제법을 확장한 것이다.
$a$와 $b$에 대해서 아래 식을 만족하는 정수 $x, y$짝을 찾아낼 수 있다.

$$ax+by=gcd(a,b)$$

계산방법

(초기조건)

$$x_0=1, x_1=0, y_0=0, y_1=1, r_0=a, r_1=b$$

(진행)

$$\begin{matrix}
q_i&\gets& |r_{i-1}/r_i|\ (i\ge 1)\
r_i&\gets& r_{i-2}-r_{i-1}\times q_{i-1}\ (i\ge 2)\
x_i&\gets& x_{i-2}-x_{i-1}\times q_{i-1}\
y_i&\gets& y_{i-2}-y_{i-1}\times q_{i-1}
\end{matrix}$$

	$x_i$	$y_i$	$r_i$	$q_i$
$i=0$	$1$	$0$	$a$
$i=1$	$0$	$1$	$b$	$\lfloor a/b\rfloor$
			$a\ mob\ b$

(예제) $15x+6y=3$을 만족시키는 $x,y$ 찾기

	$x_i$	$y_i$	$r_i$	$q_i$
$i=0$	$1$	$0$	$a=15$
$i=1$	$0$	$1$	$b=6$	$\lfloor 15/6\rfloor=2$
$i=2$	$1-0\times 2=1$	$0-1\times 2=-2$	$15\ mod\ 6=3$	$\lfloor 6/3\rfloor=2$
$i=3$			$6\ mod\ 3=0$

$r_i$이 $0$이 되는 순간 나머지가 $0$이 되는, 즉 식이 나누어 떨어지는 $x, y$를 찾았다는 의미이다.

즉, $x_{i-1}$와 $y_{i-1}$이 우리가 구하고자하는 답이다.

검산해보면,
$$15x+6y=15\times 1+6\times (-2)=15-12=3$$
인 것을 확인할 수 있다.

소스코드

int exgcd(int a, int b, int &cx, int &cy){
    if(b == 0){
        cx = 1;
        cy = 0;
        return a;
    }
    int nx, ny;
    int g = exgcd(b, a % b, nx, ny);
    cx = ny;
    cy = nx - (a / b) * ny;
    return g;
}

확장 유클리드 호제법과 모듈러 곱셈에 대한 역원을 연결해보자.

$a$의 곱셈에 대한 역원을 $x$라고 하면
$$ax\equiv 1\ (mod\ m)$$

모듈로 합동의 필요충분조건에 의해 아래와 같이 전개된다.

$$ax=1+my$$

이 식을 다시쓰면 확장 유클리드 호제법과 같은 식으로 변환할 수 있다.
$$\begin{matrix}
ax&=&1+my\
ax-my&=&1
\end{matrix}$$

그리고 앞에서 전제한 대로 $a$와 $m$이 서로소라면 아래와 같이 변경가능하다.
$$ax-my=gcd(a,m)$$

($a$와 $m$의 최대공약수가 1(즉, 서로소)이면 해가 존재하고, 그렇지 않으면 a−1은 존재하지 않는다)

따라서 $a$와 $m$에 대해서 확장 유클리드 호제법을 이용해서 $x$와 $y$를 구하면 $a$의 곱셈에 대한 역원 $x$를 구할 수 있다.

이를 이용해서 처음에 구하려던 식을 정리해보자.

다시 구하려던 식을 정리해보자.
확장 유클리드 호제법을 이용해서 $bx−my=1$ 를 만족하는 $b$의 곱셈에 대한 역원 $x$를 구하면 아래와 같이 바꿀 수 있다.
$$\begin{matrix}
(a\div b)\ mod\ m &=& (a\times b^{-1})\ mod\ m\
&=&((a\ mod\ m)\times(b^{-1}\ mod\ m))\ mod\ m\
&=&((a\ mod\ m)\times(x^{m}\ mod\ m))\ mod\ m
\end{matrix}$$

소수의 Modular 연산

소수 $17$ 사용하되, 약수인 $3$ 사용

$$\begin{matrix}
3^1, mod, 17 \equiv 3, 3^2, mod, 17 \equiv 9
\3^3, mod, 17 \equiv 10, 3^4, mod, 17 \equiv 13
\3^5, mod, 17 \equiv 5, 3^6, mod, 17 \equiv 15
\3^7, mod, 17 \equiv 11, 3^8, mod, 17 \equiv 16
\3^9, mod, 17 \equiv 14, 3^{10}, mod, 17 \equiv 8
\3^{11}, mod, 17 \equiv 7, 3^{12}, mod, 17 \equiv 4
\3^{13}, mod, 17 \equiv 12, 3^{14}, mod, 17 \equiv 2
\3^{15}, mod, 17 \equiv 6, 3^{16}, mod, 17 \equiv 1
\end{matrix}$$

---

연산의 해가 획일적으로 분포
$3$을 generator라고 한다.

만약 $3$에 어떤 지수인 $x$를 올리면 그 해는 똑같은 확률로 $0$에서 $17$사이의 하나의 정수가 된다.

단, 반대의 경우는 어렵다.
$mod$ 연산값으로 $12$이 주어지고 지수인 $13$ 찾기 어렵고, 계속 계산하는 방법 밖에 없다.

이것을 이산로그 문제라고 한다.

2. 타원곡선 (Elliptic Curve)

수학의 역사에서 타원의 둘레를 구하는 적분의 과정에서 도출된 식이라 타원곡선이라 부름

일반적으로 타원 곡선 방정식은 다음과 같다.
$$y^2+b_1xy+b_2y=x^3+a_1x^2+a_2x+a_3$$

---

실수상의 타원 곡선은 다음과 같은 특별한 범주에 속하는 타원 곡선을 사용한다.
$$y^2 = x^3 + ax + b$$

우변인 $x^3+ax+b$가 중근을 갖지 않으면, 즉 $4a^3+27b^2=0$이 아니면 타원곡선은 군(Group)을 정의 할 수 있는 대수적 특성을 제공한다.

특징

• $X$축을 중심으로 대칭
  • 어떤 $x$ 좌표 에 대해서도(정수만 사용), $X$축에 대칭 되는 두 값의 $y$을 가진다.
• 타원곡선에서 직각이 아니도록 그은 모든 직선은 곡선과 항상 3번 교차

연산

	표현	예	연산
스칼라(scalar)	소문자	p, n, a, b	덧셈, 곱셈, 역원
점(point)	대문자	G	덧셈, 곱셈

점(point)

덧셈법칙

(일반적인 좌표의 덧셈이 아니라 타원곡선 위에서의 덧셈 정의)

곡선위의 점 $P, Q$를 정해 직선으로 연결한 뒤 연장선 상에서 지나는 또 다른 점($-R$)을 찾고 이를 $X$축에 그대로 대칭시키면 곡선 위의 $R$ 좌표가 등장한다.

$$P+Q=R$$

1. 서로 다른 두점 $P+Q$

$$\begin{matrix}\lambda=(y_2-y_1)/(x_2-x_1)\ x_3=\lambda^2-x_1-x_2\ y_3=\lambda(x_1-x_3)-y_1 \end{matrix}$$

2. 같은 점 $P$

$$\begin{matrix}\lambda=(3x_1^2+a)/(2y_1)\ x_3=\lambda^2-x_1-x_2\ y_3=\lambda(x_1-x_3)-y_1 \end{matrix}$$

3. 수학적으로 이런 경우 교점이 무한대 있다고 말한다. 그리고 그점을 $O$이라고 정의하고 무한원점(point at infinity)혹은 영점(zero point)라고 부른다. 이것이 바로 이 군의 덧셈에 대한 항등원이다.

곱셈법칙

타원곡선 덧셉에 대한 정의로(같은 점) 스칼라 곱셈 연산도 표현 가능하다.

$$kP=P+P+P+...$$

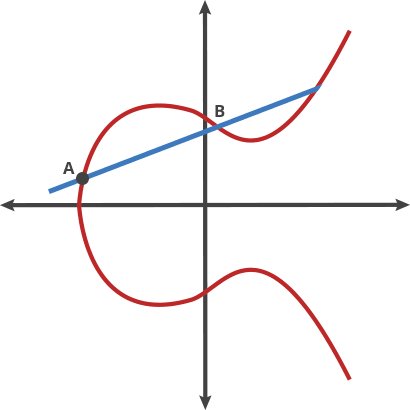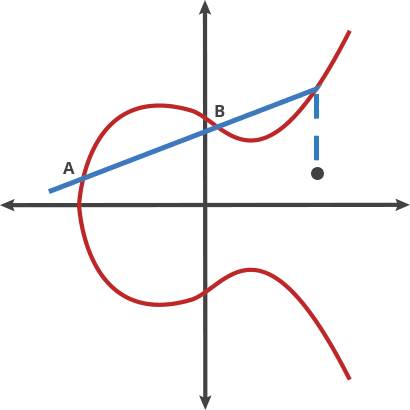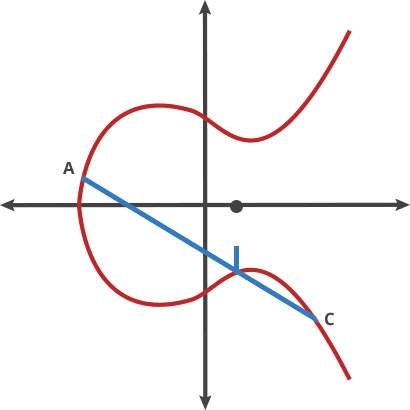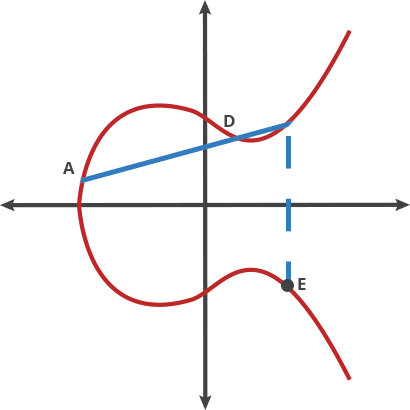
1. P에서 접선을 그려 이를 지나는 또 다른 점을 찾고, 그 대칭인 2P를 찾는다. (P+P=2P)
2. 2P와 P를 교차하는 연장선을 그어서 이를 지나는 또 다른 점을 찾고, 대칭인 3P를 찾는다. (2P+P=3P)
3. 반복
4. 덧셈을 할 때 R 의 대칭점을 취해야하는 이유를 이미 추측 할 수 있다.
   그렇지 않으면 동일한 점을 여러 번 더할때 항상 동일한 선과 동일한 세 교차점이 나타난다.

군(Group)

1. G에 속한 임의의 점 P, Q에 대해서 P + Q 또한 G에 속한다
2. (P + Q) + R = P + (Q+ R)
3. ideal point 0이 있으며 P + 0 = 0 + P = P
4. Q가 P의 역원이면 P + Q = 0
5. P + Q = Q + P

Trap door Function

점 곱셈의 특수성은 $R=k\times P$일 때 $R$과 $P$를 알고 있어도 $k$의 값을 알 수 없다.
뺼셈, 나눗셈이 없으므로 $k=R/P$로 해결할 수 없다.

3. ECC (Elliptic Curve Cryptography)

ECC는 유한 필드에 대한 타원 곡선을 기반으로하는 공개 키 암호화에 대한 접근 방식이다.

유한체(Finite Field) 상의 타원곡선(Elliptic Curve)

유한체(Finite Field)
“집합에 속해 있는 원소의 수가 한정되어 있으며, 덧셈, 곱셈 연산에 대하여 닫혀 있는 집합”을 의미한다.
“닫혀 있다” 란, 연산의 결과 값도 집합에 속해있다는 것을 의미한다.

• 암호학에서는 그래프와 부딪히는 값(k)의 추측을 더욱 어렵게 하기 위해서 정의역과 치역을 소수 p 체계로 한정한다.
• 또한 암호학에서 필수적이 속성은 그룹에 한정된 수의 포인트가 있다는 것이다(실수에 계산은 반올림 근사로 인해 느리고 부정확함). 암호화 어플리케이션은 빠르고 정확한 산술 연산이 필요하다.
• 유한체는 컴퓨터 계산에 매우 적합하므로 타원곡선에 사용된다. ECC는 p를 가지고 mod 연산을 하는데 이는 유한체이다.
• 참고로, 타원곡선이 암호학에 적합한 이유는, 실수(Real Number)상에서 연산을 하든, 유한체 상에서 연산을 하든, 동일한 수학법칙이 적용되기 때문이다.

수식

$$y^2 \equiv (x^3 + ax + b),, mod, p$$

집합

$$E(F_p) = \left{(x,y)|y^2=x^3+ax+b\right}\cup \left{O\right}$$

특징

• 방정식에 $mod\ p$하면 $y^2$의 값은 $0$에서 $p-1$이다.
• 정수만 사용하고 있기 떄문에, 사각수(제곱수)는 작은 그룹이며 가능한 점들의 갯수를 $N$이라고 한다. ($N<p$)
• 어떤 $x$ 좌표에 대해서든 두 점을 가지기 때문에, 가능한 $x$ 좌표는 $N/2$개 이다. 즉, 이 타원 곡선은 유한 한 수의 점을 가지고 있다.(정수 계산과 modular 때문)
• 이렇게 바뀐 타원곡선함수는 곡선이 아닌 점들이 뭉쳐 있는 구름 형태이다.
• 암호학에서는 타원곡선의 난이도를 높이기 위해 곡선에 부딪히는 횟수도 소수 단위로 한정한다.
• 또 일정한 한계치 값을 넘치면 새로운 값에서 함수를 시작시키는 등 제약을 도입하게 되는데 이렇게 추가적으로 암호화한 값은 해독하기가 매우 어렵다.

Example

$$E: y^2=x^3+x \ over\ Z_{23}\ (p=23)$$

만약 $x=9$라고할 때 $y^2\ mod\ 23=(729+ 9)\ mod\ 23=738\ mod\ 23=2$이다.
이때 만족하는 $y$는 $5*\ mod\ 23=2$이므로 $y$는 $5$가 될 수 있다.

이때 갈루아 필드의 $p$가 조금만 더 커지면 우리는 $y$를 쉽게 찾을 수 없게 된다.
따라서 이를 통해 암호학에 적용 할 수 있게 된다.

)

4. ECDSA (Elliptic Curve Digital Signature Algorithm)

비트코인 등 블록체인 기반 기술에서는 키 쌍의 생성에 ECDSA를 사용하여 키 길이 256 비트 이상을 사용한다.
미국국립표준기술원(NIST)에서 개발한 secp256k1 표준에 정의된 타원 곡선을 사용한다.

$$y^2\ mod\ p=(x^3+7)\ mod\ p$$
$$p=2^{256}-2^{32}-2^9-2^8-2^7-2^6-2^4-1$$

Domain Parameters(secp256k1)

	값	설명
p	FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE FFFFFC2F	modulo prime number
a	00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000=0	방정식 계수
b	00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000007=7	방정식 계수

	값	설명
G	02 79BE667E F9DCBBAC 55A06295 CE870B07 029BFCDB 2DCE28D9 59F2815B 16F81798 (compressed form)	Base Point/Generator Point
n	FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE BAAEDCE6 AF48A03B BFD25E8C D0364141	order of point G(G를 n번 더하면 무한원점이 되는 값)
h	01	cofactor

1. 총 점의 수 N값은 Schoof's algorithm을 통해 구한다(Hasse's theorem on elliptic curves과 중국인의 나머지정리를 기반으로 만들어짐).
2. 전체 집합 원소의 수 N에서 부분집합의 수인 n을 결정한다(n은 소수이면서 N의 약수).
3. 보조 인자(cofactor)인 $h=N/n$ 를 구한다.
4. 타원곡선 위 임의의 점 $P$를 골라서 기준점 $G=hP$를 구한다.
5. $G$가 $0$이면 다른 $P$를 골라서 반복한다.

기본 원리

1. 타원곡선에서 임의의 점(Point of Origin)을 선택한다.
2. 임의의 숫자(Private Key)를 생성한다.
3. 원점과 임의의 숫자를 사용하는 마법의 수학 방정식을 쓰면 타원곡선 위에서 두번째 점(Public Key)이 된다.
4. 파일의 Hash와 함께 이 Private Key를 마법의 방정식에 넣으면 서명이 부여된다. 서명은 R과 S 두 부분으로 나뉜다.
5. 서명이 올바른지 확인하려면 Public Key,S,R를 또다른 마법의 방정식에 넣으면 R이 나오는 것을 확인한다.

(1) Private Key (d)

RSA와 달리 Private Key를 먼저 정한다.
난수생성기를 사용하여 ${1, ..., p-1}$ 범위 중 랜덤 integer $d$를 선택한다. (20 bytes=160 bit)

$y^2=x^3-2x+15$
$G=[4,5]$
$d_A=3$

(2) Public Key (Q)

타원곡선의 publlic key는 generation point인 시작점 $G$가 private key에 해당하는 숫자, $d$만큼 타원곡선 상의 덧셈 연산을 실행해 곡선에 안착한 좌표, $Q$에 해당한다

$$Q(x,y)=d\times G(x_0, y_0)$$

$G$는 이미 알려져있고, $Q$는 Public Key 생성 후 공개되지만, 이 두 값으로 $d$를 유추해 내기 굉장히 어렵다(ECDLP,Elliptic Curve Discrete Logarithm Problem).
직접 대입 방식 말고는 아직까지 해답이 없다.

$Q_A=d_A_G=3_[4,5]=[13,22]$

(3) Sign

• 파일의 해시(파일 고유 번호)와 함께 개인키를 방정식에 넣으면 서명됨
• 서명은 각각 20바이트의 $r$과 $s$ 두값으로 나뉨 $(r,s)$

$r$

1. 먼저 임의의 값인 '$k$(20 bytes)'를 생성하고 점의 곱셈을 사용하여 $P=k\times G$를 계산한다.
2. 점 $P$의 $x$값이 '$r$'을 나타낸다(20 bytes).

$s$

1. $s$를 계산하려면 메시지의 SHA1 해시를 만들어야한다. 이 값은 매우 큰 정수로 간주되는 20 bytes 값을 제공하며 '$z$'라고 한다.
2. 다음 등식을 사용하여 $s$ 를 계산할 수 있다.

$$s=k^{-1}(z+dA\times r)\ mod\ P$$

(4) 검증

public key만 있으면 가능하다.
아래 방정식을 통해 점 P를 계산한다.

$$P=s^{-1}\times z \times G+s^{-1}\times r \times Qa$$

점 $P$의 $X$좌표가 $r$과 같으면 서명이 유효함을 의미하고 그렇지 않으면 유효하지 않다.

검증식 증명

검증식이 서명식으로 전개되는 것을 증명한다.

$P=s^{-1}\times z \times G+s^{-1}\times r \times Qa$
$(Qa=dA\times G)$
$P=s^{-1}\times z \times G+s^{-1}\times r \times dA\times G$
$k\times G=s^{-1}(z+dA\times r)\times G$
$k=s^{-1}(z+dA\times r)$
$s=k^{-1}(z+dA\times r)$

(5) Public Key Recover (Ethereum)

For $j$ from $0$ to $h$ do the following.

1. Let $x = r + jn$.
2. Convert the integer $x$ to an octet string $X$ of length $mlen$ using the conversion routine specified in Section 2.3.7, where $mlen = \lceil(log_{2} p)/8e\rceil$ or $mlen = \lceil m/8e\rceil$.
3. Convert the octet string 0216kX to an elliptic curve point R using the conversion routine specified in Section 2.3.4. If this conversion routine outputs “invalid”, then do another iteration of Step 1.
4. If $nR \ne O$, then do another iteration of Step 1.
5. Compute e from M using Steps 2 and 3 of ECDSA signature verification.
6. For k from 1 to 2 do the following.
   1. Compute a candidate public key as:
   2. $$Q=r^{-1}(sR-eG)$$
   3. Verify that $Q$ is the authentic public key. (For example, verify the signature of a certification authority in a certificate which has been truncated by the omission of $Q$ from the certificate.) If $Q$ is authenticated, stop and output $Q$.
   4. Change $R$ to $-R$.

go-ethereum/crypto/secp256k1/secp256.go

// RecoverPubkey returns the public key of the signer.
// msg must be the 32-byte hash of the message to be signed.
// sig must be a 65-byte compact ECDSA signature containing the
// recovery id as the last element.
func RecoverPubkey(msg []byte, sig []byte) ([]byte, error) {
    if len(msg) != 32 {
        return nil, ErrInvalidMsgLen
    }
    if err := checkSignature(sig); err != nil {
        return nil, err
    }

    var (
        pubkey  = make([]byte, 65)
        sigdata = (* /*line :103:15*/_Ctype_uchar /*line :103:22*/)(unsafe.Pointer(&sig[0]))
        msgdata = (* /*line :104:15*/_Ctype_uchar /*line :104:22*/)(unsafe.Pointer(&msg[0]))
    )
    if func() _Ctype_int{ _cgo0 := /*line :106:35*/context; var _cgo1 *_Ctype_uchar = /*line :106:44*/(*_Ctype_uchar)(unsafe.Pointer(&pubkey[0])); var _cgo2 *_Ctype_uchar = /*line :106:84*/sigdata; var _cgo3 *_Ctype_uchar = /*line :106:93*/msgdata; _cgoCheckPointer(_cgo0); return _Cfunc_secp256k1_ext_ecdsa_recover(_cgo0, _cgo1, _cgo2, _cgo3); }() == 0 {
        return nil, ErrRecoverFailed
    }
    return pubkey, nil
}

보안

• $s$를 계산하려면 '$k$'(난수)와 '$dA$'(개인 키)가 필요하지만 서명을 검증하기 위해서는 $r$과 $Qa$(공개 키)만 있으면 된다.
• $r=k_G$ 와 $Qa=dA_G$ 그리고 ECDSA 포인트 곱셈에서 트랩 도어 기능으로 인해, $Qa$와 $R$을 알지 못하여 $dA$ 또는 $k$를 계산할 수 없으므로 보안적으로 안전하다.
• 개인 키를 찾을 수있는 방법이 없으며 개인 키를 모른 채 서명을 위조 할 방법이 없다

Reference

https://noasax.github.io/problem%20solving/2017/09/24/Division-in-modular.html
https://www.weeklyps.com/entry/%EC%9C%A0%ED%81%B4%EB%A6%AC%EB%93%9C-%ED%98%B8%EC%A0%9C%EB%B2%95-%EC%B5%9C%EB%8C%80%EA%B3%B5%EC%95%BD%EC%88%98-%EA%B5%AC%ED%95%98%EA%B8%B0?category=795989
https://www.instructables.com/id/Understanding-how-ECDSA-protects-your-data/
https://www.mk.co.kr/news/economy/view/2019/03/168095/
http://slidesplayer.org/slide/11329530/